What are PINNs?

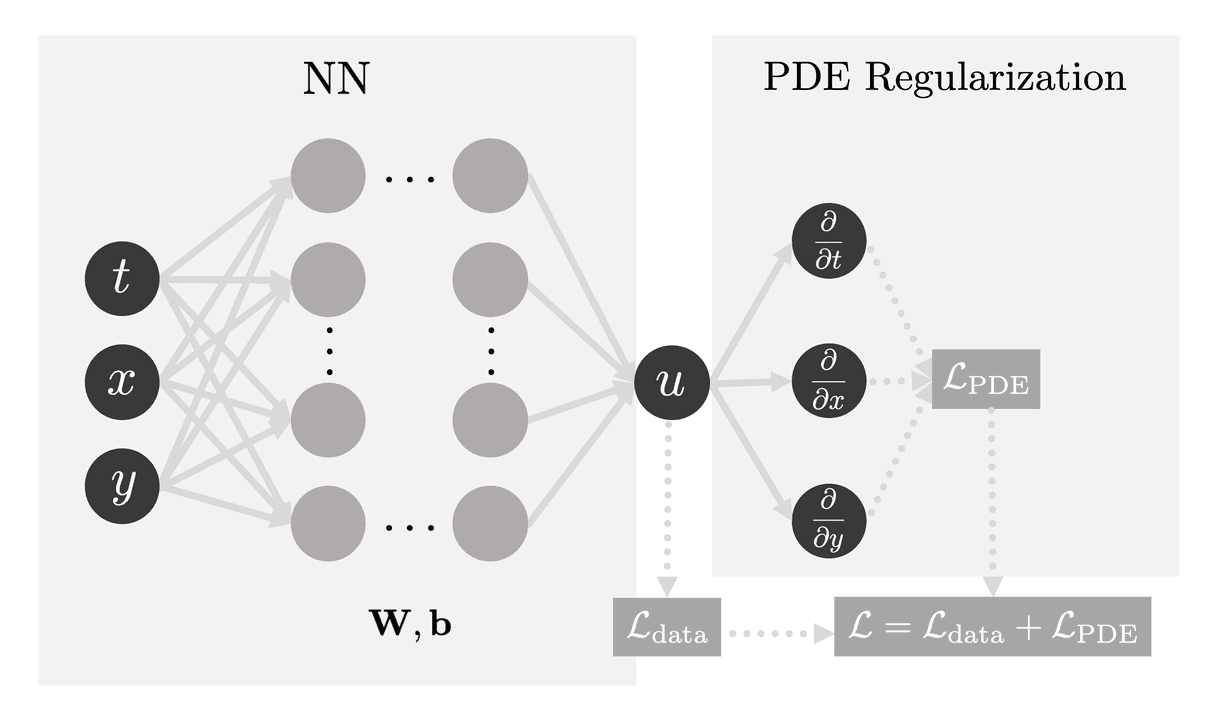
Physics-Informed Neural Networks (PINNs) combine the fundamental laws of physics with the predictive capacity of machine learning, thereby transforming the area of computational science. By integrating differential equations that represent physical rules in standard loss functions, they enable them to predict outcomes for complicated systems when standard models would not be able to.

Embedded physical principles steer the network towards physically feasible solutions, minimizing the reliance on big datasets. This makes PINNs particularly useful in situations when data is expensive or limited. In fields where it is essential to comprehend system behavior under varied conditions, such as fluid dynamics, material science, and geophysics, they are very helpful.

PINNs application using 2D Heat equation

Heat transfer equation in 2D

A fundamental concept in thermodynamics and heat transfer, the 2D heat equation shows how heat diffuses through a certain area over time. Traditionally, numerical techniques such as finite element or finite difference analysis have been used to solve problems. Although these techniques are efficient, they can be computationally demanding and time-consuming, particularly when dealing with complicated geometries and boundary conditions.

By presenting the 2D heat equation as an optimization problem, we may take use of neural networks' flexibility and effectiveness. The basic goal is to train a neural network without the necessity for a mesh-based discretization of the domain to approximate the temperature distribution in a domain given initial and boundary conditions.

Imagine we're working with two outputs, a and b, for which we lack specific target labels. However, we understand these outputs must adhere to the principles of physics. To ensure this adherence, we introduce a penalty in the form of a regularizer whenever a and b deviate from these physical laws. This penalty serves as a guiding signal, allowing the network to learn and internalize the fundamentals of physics.

The problem of solving 2D heat equation can be divided into two types:

Overall Process:

Fun Fact: You don’t need very big models or LLMs to train such a network. A simple fully connected network with just 100-150 learnable parameters is sufficient to solve this problem.

In our next blog in this series, we will be diving deep in the heat equations for the simple case of a 2D plate and implement a neural network that can learn the physics it in PyTorch.