What are KANs and what can they do?

Figure 2.1 in the KAN paper from Ziming Liu et al.

KANs are based on the Kolmogorov-Arnold representation theorem, which says that if 𝑓 is a multivariate continuous function on a bounded domain, then 𝑓 can be written as a finite composition of continuous univariate functions and the binary operation of addition. Putting it mathematically:

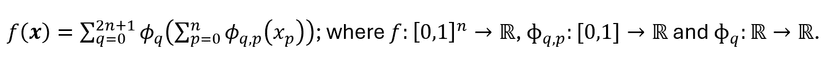
A multivariate continuous function can be written as a finite composition of continuous univariate functions

The equation looks complex, but it is just a function which takes a vector input x (hence multivariate), and gives out a real valued output (which is by definition of any function). It does so by applying only univariate functions (or single variable functions) ϕ as described above, and summing up the outputs of these ϕ's.

Why is this relevant? Well, because this is equivalent to the Universal Approximation Theorem - the theoretical bedrock of the neural networks we have come to know and love - which theoretically guarantees that we can approximate any possible continuous function arbitrarily well enough, given we have a complex enough neural network.

KANs are basically a way of extending the concept of the above equation (which can be thought of as a KAN which is 2 layers deep. This will become more clear in a diagram later), and being able to make arbitrarily deep networks.

You may wonder that if a 2 layer KAN can represents that equation, which can in turn learn any function, why do we need deeper KANs? Well because there is a catch. We can’t use the power of the Kolmogorov-Arnold representation theorem as the continuous univariate functions ɸ in the original equation above are allowed to be non-smooth and even fractal, which may not be learnable in practice. Hence, we will need more layers to learn more complex functions.

Why should we care about KANs?

Well, they are a novel way of thinking about neural networks, which are in essence high dimensional function approximating black boxes. They also offer certain advantages over MLPs, the main advantages being:

1. Better performance with lesser number of parameters than MLPs.
2. Explainability! something that has been missing from deep neural networks.

B-splines

Before proceeding to the details of the KAN, we first need to get a feel of the concepts of B-splines. Imagine you're drawing a curve on a piece of paper. Normally, you might use a pencil and just sketch it out. But what if you wanted to draw a really smooth curve that goes through specific points? That's where B-splines come in! B-splines are a way of creating smooth curves that pass through a set of ‘control points’.These control points are basically points that define the shape of the curve. The curve itself is made up of smaller segments called "splines".

Now, here's where it gets interesting: the degree of the B-spline determines how the curve behaves between the control points. If the degree is low, like 1 or 2, the curve might bend sharply between points. But if the degree is higher, like 3 or 4, the curve will be smoother and flow more gracefully between the points.

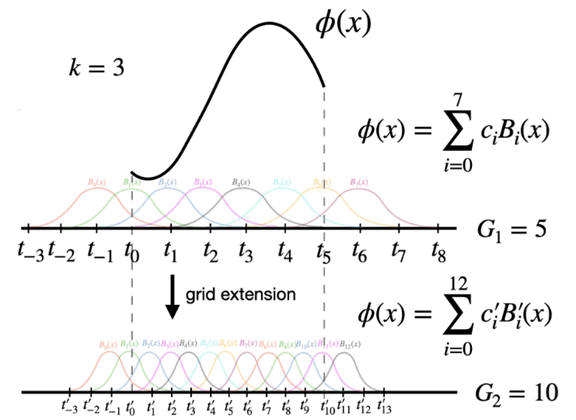
Figure 2.2 from the KAN paper, zooming into an edge of the KAN

In the above figure, ɸ(x) is the black curve, which is formed by using a weighted sum of the control points c(i)'s corresponding to points t(i)'s on the x-axis. The weights are determined by something called the Basis functions B(i)'s (the curves in color below the black curve). Notice that when x=t(0), B1(x) i.e. the green curve, has the maximum value, hence the control point c(0), has the maximum weightage and hence influence on ɸ near point t(0). Similarly you can see that the influence of say c(7) is 0, while c(3) is a small non zero value.

Now that you understand that control points essentially form the shape of the curve, and that at the end of the day we need to learn some continuous function, can you guess what the learnable parameters of KAN are? Well of course the c(i)'s! The basis functions on the other hand are ugly looking recursive functions, and you can check it out here. Furthermore, as you can guess higher the number of ‘grid points’ (G given in the above graph), better the approximation of the underlying curve.

Finally, the Kolmogorov-Arnold Network

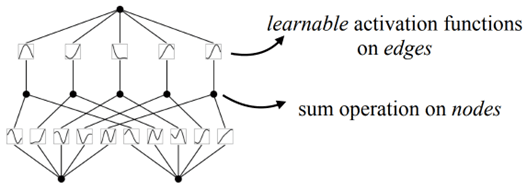
A two layer network with input dimension = 2, hidden dimension = 5, and output dimension = 1.

The original equation described in the first section can be depicted as a 2-layer KAN as shown above. The nodes are where the summation operation takes place, and the learnable activations ɸ are on the edges, in contrast to MLPs where the edges have learnable weights instead, and the activation is fixed and is performed on the nodes.

The authors define ɸ(x) as given above, and spline(x) is parametrized as a linear combination of B-splines as we discussed before this section. They include the w as a factor to better control the overall magnitude of this activation function. They also update the grid (size G) on the fly according to its input activations, to address the issue that splines are defined on bounded regions (for example t(0) to t(5) in the previous sections spline curve diagram) but activation values can evolve out of the fixed region during training.

Furthermore, the authors give a proof giving a theoretical upper bound to the error between the actual function and the learned function of the network, which **drum rolls**, is independent of the dimension of the data (and actually depends on the grid size G)! This is good news as KANs are less prone to the Curse of Dimensionality than MLPs (they are still prone to it, because of constant factor C in the upper bound which may be dependent on the dimension of the data. The authors leave that investigation to future work).

Assuming L layers of equal width N, and with each spline of degree (usually k = 3) with G grid points, there are in total O(N^2*L*(G+k)) ∼ O(N^2*L*G) parameters. In contrast, an MLP with depth L and width N only needs O(N^2*L) parameters, which appears to be more efficient than KAN. But, KANs require much smaller N than MLPs, which not only saves parameters (at the cost of more complex optimization of the network), but also achieves better generalization and facilitates interpretability.

When we say it facilitates interpretability, it is in the sense that you can prune the network to remove edges and nodes which don't contribute much to the network, and can substitute the activations by their corresponding univariate lookalikes. So if an activation on an edge seems to behave like a sine wave, we can fit a sine function using linear regression, and finally see a composition of such univariate functions making the target function or the function that the KAN represents! You can check out the implementation details of how the authors do it on their GitHub repo here.

Sparsification of the network and subsequent pruning using a thresholding technique is discussed in the paper, and not too complicated. The authors propose regularization using L1 norm, but define the L1 norm for activations instead of weights like we usually do in an MLP.

Final Thoughts

While the idea of KANs look promising, we take it with a pinch of salt, mainly because of the two following reasons

1. The authors do not show any experiments with real world datasets, not even the MNIST dataset which is the first dataset beginners use when starting off with computer vision. They only use toy examples, trying to fit the model to data generated by complex mathematical equations (and do find interesting results which you should check out in the paper).
2. The authors don't give any details of training any network deeper than 5 layers. We may give them the benefit of the doubt that there doesn't exist any optimized libraries available to efficiently build deeper KANs, but the promise of KANs is yet to be seen in real world applications, and whether they can replace the already extremely efficient MLP.

The authors also do mention that training is 10x slower than MLPs, which is the cost of learning more accurate and interpretable functions. While it is too soon to claim that this paper is as revolutionary as backpropagation or attention is all you need, there certainly seems potential in this novel approach of looking at neural networks. Let us know your thoughts in the comments and any interesting observations you got if you got a chance to use KANs!